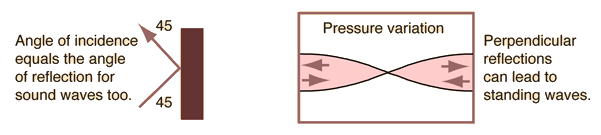
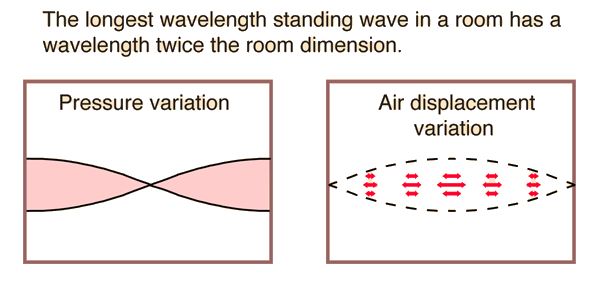
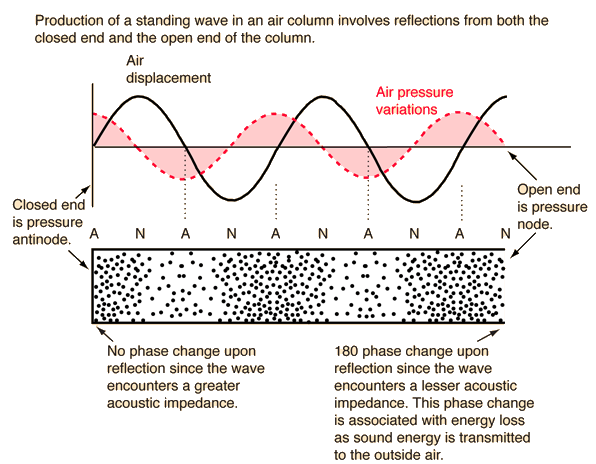
This application note is intended as a general guideline in the selection and specification of coaxial cables for applications requiring phase matching and or phase tracking versus temperature. The match can be specified in electrical degrees as in the suggested best match curves of Figure 1 or in nanoseconds of time delay.
Figure 1. Suggested Phase match limits
M/A-COM Antennas, Cables and Waveguides
The M/A-COM Antenna, Cable and Waveguide (ACW) product line has developed hundreds of various cable sizes/constructions each optimized for different applications. Most utilize solid or air-spaced PTFE dielectrics and fall into four general families that can be characterized by their Velocity of Propagation (Vp):
69% Velocity of Propagation
76% Velocity of Propagation
80% Velocity of Propagation
82% Velocity of Propagation
Cables with a solid extruded PTFE dielectric core have a nominal Vp of 69% and are generally the strongest mechanically but worst for insertion loss and phase changes as a function of temperature. Cables with a high air content and a nominal Vp of 82% are generally weaker mechanically but the best electrically with very low insertion loss and excellent phase versus temperature characteristics.
Cables with intermediate values of Vp, Vp of 76% for example, are offered as a balance between mechanical and electrical parameters and have proven to be very reliable in over 40 years of service in demanding military programs. Typical phase-temperature characteristics for these families are illustrated in Figure 2.
Figure 2. Phase versus temperature characteristics for common cable families
Although based on M/A-COM cables, these curves are also representative of cables from all cable manufacturers. The nominal Vp for any particular cable type is given in its data sheet.
Coaxial Cable Phase Matching
The closeness of the match in phase matched cable sets is dependent upon several parameters. These include:
1. Highest Frequency of Operation
In general, the higher the operating frequency, the more difficult it is to achieve a close match. The match limits of Figure 1 are generally offered with minimal extra cost for the additional fabrication and testing required. More stringent matches may require even greater effort and cost, or the use of phase adjustable connectors.
2. Length of Cable Assembly
The longer the cable assembly, the more difficult is the matching task. Thus, longer assemblies require wider phase match windows. Conversely, short assemblies can often be provided with tighter phase match windows. The suggested "Best Match" limits can readily be achieved for assemblies of the specified lengths, and sometimes longer. With increased
manufacturing effort, and corresponding increase in price, tighter limits can be achieved. It is often necessary to balance system requirements and financial restrictions to arrive at the best solution.
3. Variation of Velocity of Propagation
Cables which have identical physical lengths but different Vp's will have different electrical lengths. Tight control of Vp eases the matching process and results in assemblies with more similar physical lengths. For high Vp flexible coaxial cable assemblies the Vp can usually be held to the nominal value within ±1% about half of the specified ±2% range. For long assemblies, adjustment of the physical length to achieve match can result in a variation of several inches. Thus, it is best to specify the electrical match and minimum mechanical length with length being the variable to achieve the desired phase match. Specifying both a tight phase match tolerance, and a tight length tolerance, decreases cable yield and increases cost.
Consider as an example a ten foot assembly for use up to 18 GHz. Further, assume that it has a nominal Vp of 82% but due to manufacturing or material variations, the Vp can range from 81.0% to 83.0%. Recall that in free space
C=f * λ
Where C is the speed of light approximately 3 * 108 meters/second, f is the frequency in Hertz, and λ is the free space wavelength in meters. At 18 GHz, the wavelength is 0.0167 meters. Within the coaxial cable, the effective wavelength is Vp * λ or 0.0137 meters. Our hypothetical ten foot cable with Vp of 82% is 223.1 wavelengths long. Each wavelength is a 360 degree phase shift so the electrical length is around 80,316 degrees.
If we repeat the calculation with Vp reduced to its 81% limit, the effective wavelength is 0.0135 meters. The same ten foot length is now 225.8 wavelengths long with a corresponding phase shift of around 81,288 degrees.
The M/A-COM Cable Catalog program includes a calculator that illustrates this phenomenon by calculating the phase difference between two identical length cables having different Vps. The numbers are a bit different from the sample calculation because more decimal places are used in the program. Note the dramatic effect a small change in Vp has on the electrical length. It also calculates the length change required to phase match the cable pair. The required length adjustments are shown in Figure 3 below.
 |  |
| Figure 3a. Comparison of cables with Vp = 82.0% and 81.0% | Figure 3b. Comparison of cables with Vp = 82.0% and 83.0% |
Figure 3. Length adjustment to match 10' cables with Vp ranging from 81.0% to 83.0%.
Note that phase matching under these conditions requires a length tolerance of ±1.5 inches, which is not obvious. Our intuition might say use ±0.12 inches to achieve a good match. But a tight length restriction only limits the amount of cable that can be used to fabricate the matched cables and doesn't assure a match. In fact, as shown in this example, cables with precisely the same length have a phase variation due to different Vps of approximately 980°.
4. Temperature
The electrical length of a Teflon dielectric coaxial cable assembly changes as a complex function of temperature as shown by the phase-temp curves of Figure 2. Note that over most temperature ranges the higher Vp cables exhibit smaller phase changes than the lower Vp cables. This is also important in Phase Tracking, which is discussed in the next section.
Suppose two ten foot assemblies are perfectly matched to each other at room temperature. Now suppose one cable of the pair is used in a temperature controlled area while the second cable is used in an area where the temperature varies from -55°C to +125°C. Using the formulas given in Section 3 above, combined with the phase-temperature changes given in Figure 2, we can determine the electrical length at any temperature.
Consider a solid Teflon dielectric with Vp of 69%. At room temperature the phase shift is 95,482°. At -55°C the length increases by 294°; at +125°C it decreases by 162°.
If the dielectric were air-spaced Teflon with Vp of 82%, the numbers are quite different. The room temperature phase shift is 80,345°. At -55°C the length increases by 26°; at +125°C it increases by 57°; and at 30°C the length decreases by 1°.
Again, this calculation has been automated with a calculator, which is illustrated in Figure 4.
Figure 4. Phase shift change over temperature range Clearly, special precautions must be taken to maintain the match when the cables of a matched set are exposed to different temperatures.
5. Connectors
It is much easier to phase match cable assemblies with the same connectors on both ends than assemblies with different connectors. That doesn't mean that an assembly with straight connectors can't be matched to one with
angled connectors; or one with TNC connectors matched to one with SMA connectors. It just adds to the difficulty and uncertainty of the match.
In some applications it is necessary to account for the phase changes which occur during installation.
Often the system software does this. It can also be accomplished through the use of phase adjustable connectors attached directly to the cable assembly.
6. Test Equipment Accuracy
It is highly recommended that a Vector Automatic Network Analyzer or PNA (Agilent 8510 for example) be used for the measurement of electrical length. To achieve a high degree of accuracy, the test equipment and cable assemblies must be stabilized in a temperature-controlled room. At M/A-COM we do the final phase trimming and ATP testing in the same temperature controlled room.
Cable Matched Sets
When the cables of a matched set are bent into different shapes in their installed condition, test fixtures simulating the installation bends should be used during the matching process.
Matching in Sets
There are two ways of phase matching sets of cables:
Matched to a Standard
Matched to other cables in the set
Matching to a Standard
The phase standard could consist of either a "Gold" hardware standard or an unchanging software standard; i.e. a known electrical length in degrees at a specific frequency. Cable assemblies that are phase matched to a gold standard are completely interchangeable. Similarly, cable assemblies that are phase matched to a software standard (known electrical length) are also completely interchangeable. In addition the use of software standards is more cost effective since they don't require extra material to produce physical standards. With this approach any cable of a set can be replaced without replacing all cables of the set.
Matching as a Set
Cable assemblies matched as a set are only guaranteed to be matched to other cables in the same set. There is no guarantee that the cables in any one set will match those of another set, especially if they are manufactured at different times. This approach results in the lowest cost because cable yields are highest. The drawback is that should any one cable of a set have to be replaced, the entire set may be replaced.
Specifying Phase Matched Sets
To produce phase matched sets the manufacturer needs as much of above information as you can provide. At a minimum we need to know which cables make up the set, the highest frequency of operation and the desired match. We also need to know if phase standards are required. For critical applications we need to know the bends of the installed configuration so the matching is achieved simulating the installed configuration. This is especially true of long cables where one or more cables might be coiled while others are relatively straight.
Phase Tracking
Phase tracking is primarily influenced by three parameters:
Temperature
Bends
Preconditioning
Temperature changes
The overall phase tracking due to temperature changes is dependent upon whether all assemblies in the set are exposed to the same thermal environment. The absolute phase change is dependent primarily upon the velocity of propagation. In general, the less the absolute phase changes, the better the phase tracking over temperature. Thus, higher Vp cables are less sensitive to phase temperature changes and track better. This was shown in the examples above.
Bends
The overall phase tracking due to bends is extremely difficult to predict. For static installations, it depends upon the number of bends, the angular arc they encompass and the proximity to other bends. For dynamic installations, it depends upon the similarity of the flexure cycle each cable experiences.
Preconditioning
Prior to matching the cables of a phase-matched set it is necessary to thermally stress relieve them to assure good tracking. For example, assume that the first time a cable assembly is exposed to 125°C its phase shift changes by 10 degrees. The second time this might be reduced to 8 degrees; the third time, 7.5 degrees; the fourth time, 7.2 degrees; etc. Thus, thermal cycling artificially ages or stabilizes the assembly. All M/A-COM phase matched cable assemblies are preconditioned prior to final matching.
The tracking deviation is dependent primarily on the similarity of the installation for each cable in the set. To achieve the best phase tracking it is necessary that all cables be installed in a similar manner, be exposed to the same thermal environment and/or be flexed together.
Critical Applications
For critical applications where the ultimate tracking is required, the cables of the phase-matched set should be stranded into a bundle and enclosed within a protective sheath. If possible, the sheath should be a thermal blanket that maintains the temperature near 30°C where temperature sensitivity is minimal.
ELABORADO POR:
NERWIN ANTONIO MORA REINOSO
C.I: 17.557.095
CAF
Carbon nanotubes hold great promise due to their extraordinary electrical, mechanical, optical, thermal, and chemical properties. Their current applications range from improving consumer electronics, to medicine delivery to cells, to strengthening airplane components. Carbon nanotubes come in many different forms and purities. They range from flexible, thin, few-walled or single-walled nanotubes (SWNTs) to rigid, long, thick, multi-walled nanotubes (MWNTs), with a spectrum of characteristics.
